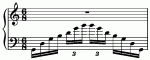Warning: this post may contain traces of moth
Warning: this post may contain traces of moth
Spent the day at Senate House Library (the music bit), on one of my regular-ish trawls for new stuff to include in modules about music for dance teaching. It’s a very odd and frustrating corner of the musical universe that I plough, and looking for relevant recent research was, as usual, a bit like doing Christmas shopping – you find loads of things that you’d like for yourself, or for people that you never buy presents for; or many things that would suit the same person.
There was one rather satisfying find though: Peter Van der Merwe’s book The Roots of the Classical: The Popular Origins of Classical Music, which has a useful chapter on ‘The Dances of Central Europe’. Bear with me as I explain why (or don’t – this won’t be funny):
Students of mine (and patient friends who have to listen to this kind of thing in the pub) will know that I’ve coined the rather clumsy phrase ‘truly triple metre’ to distinguish those dances which don’t fall victim so readily to what Rothstein called the ‘great 19th century rhythm problem‘. And my idea of punishment is having to explain to people what ‘the difference between 6/8 and 3/4’ is, because for as long as one bar of 3/4 is part of a set of two bars of 3/4 (which they mostly are) there is no audible difference. The only difference is one of notation, and unless you’re fluent in music notation, what’s the first thing you ask – ‘can you play it to me so I can hear it’. But the whole point is, you can’t hear it, no more than you can feel the arctic circle.
Now Van der Merwe has this rather cute theory: he reckons that as the waltz developed in the 19th century, ‘the basic, unrepeated waltz strain (in other words, the bit before the double-bar line) now takes up sixteen bars instead of eight’. The only way for the waltz to expand any further, he argues, was ‘by repeated doubling, like an organic cell’ (Growth by doubling, p. 250). Now I agree with his end result, but I don’t quite agree with how he gets there. I think he’s right, but I think he’s right because it’s the basic ‘unit’ of the waltz which has doubled itself from something containing three steps (in the non-dance sense of the word), into two sets of three steps subsumed into a duple hypermeasure, which then far more readily accrues more duple hypermeasures.
All of which is far too complex a hammer to crack a simple nut – it’s only a waltz, after all. Far too complex, until you look, as I did this morning by chance, at a moth, whose mirror-symmetrical wings illustrate perfectly the expansion of two triple units into a hypermetrical duple thingy, which itself is just a ‘thing’. Each wing is roughly speaking a ‘triple’ thing, because the proportion of the segments is 2:1, and that’s what music in 6/8 often tends to do. It’s when the symmetry is missing – e.g. if the second half of the bar were simply, contour-wise, to be a repeat of the first, in a kind of saw-tooth shape, then you’ve got a saw-tooth, not a moth – in my terms, truly triple metre.
Ah well, back to the ironing.